코딩테스트 합격자 되기 - 03 알고리즘의 효율 분석

 

 

 

• 문제에 맞는 알고리즘을 선택하는 것이 중요하다. 이 때 기준은 시간복잡도이다.
• best case, average case, worst case 가 있지만 제한 시간 내에 결과 값이 나와야 하는 코딩테스트의 목적에 부합한 최악의 상황을 기준으로 시간 복잡도를 측정해야 한다.
• f(x)의 최악의 시간 복잡도는 O(g(x))라고 쓴다. (빅오 표기법)

 

 

---

 

• 점근적 상한 : 특정 지점부터 항상 내 연산회수보다 위에 있는 함수들 중 하나를 사용하면 된다. (빅오 표기법을 사용한다)
• 위의 예시 y=x^2+3x+5 일 때 O(x^3), O(2x^2) 모두 사용이 가능하지만 조금더 의미 있는 점근적 상한 하나를 정해야한다. 

 

 

• 최고차항의 상수 및 부호를 떼고 나머지를 버리면된다. -> O(x^2) 
• 최고차항 보다 높은 차수는 오차가 너무 크므로 의미가 없다. (예를들어 연봉 5000인데 대기업회장보다 적게받습니다. 라고 말하는 것과 비슷하다고한다 ㅎㅎ)

 

---

 

시간복잡도 활용하기

입력값을 보고 시간복잡도를 예상하고 사용할 자료구조를 예측할 수 있다.

 

• 배열 인덱스를 통한 원소 접근 : O(1)
• 트리탐색 (이진탐색) : O(logx)
• 선형탐색 (순차탐색) : O(x)
• 정렬 : O(nlogn)
• 행렬곱셈 (이중배열, 다항식계산) : O(x^2)
• 부분집합 (하노이) : O(2^x)
• 순열 (외판원문제) : O(n!)

 

 

• ex1) 문자열의 길이 1,000,000 이하의 자연수
  • --> O(N^2) 은 최대 연산회수 3000~ 이다.
  • --> O(N^2) 알고리즘으로 풀면 통과 하지 못한다! 추측
• ex2) 회전 횟수 n은 자연수이며 1~4입니다.
  • --> 복잡한 알고리즘을 생각하지 않고 그냥 구현하면된다! 추측

 

---

 

저자와 함께하는 스터디 - 1주차 과제 공지 (네이버카페)

코딩테스트 합격자 되기 - 03 알고리즘의 효율 분석

 

Q. f(x) 수식들을 만족하는  f(x) <= C*g(x) 를 만족하는 C를 구하기! 실제 특정 시점부터 넘는지 확인할 수 있도록 그래프 제시하기!

1. 3x^2 + 5x + 6

• 빅오표기 : O(x^2)
• 3x^2 + 5x + 6 <= 4x^2

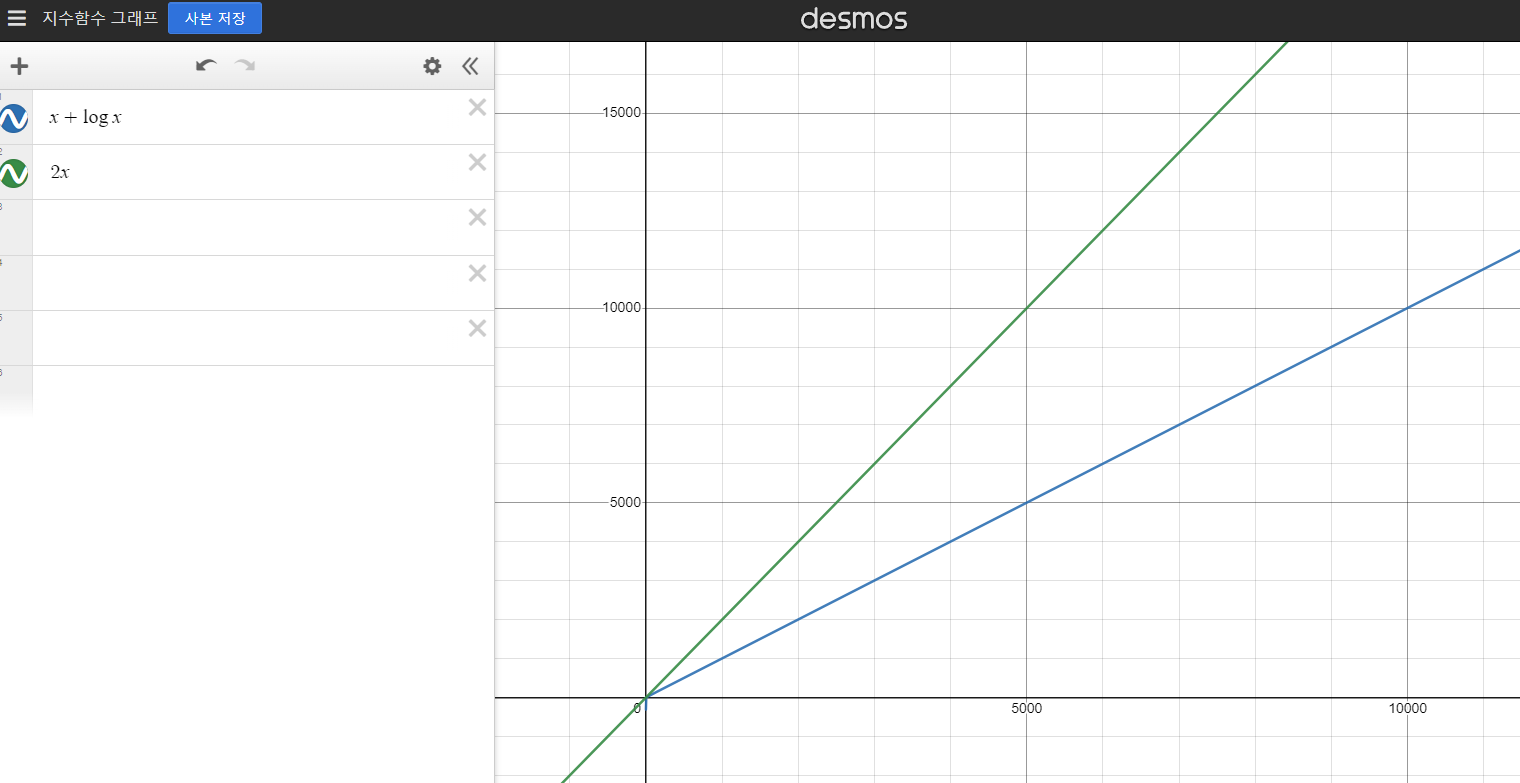
2. x + logx

• 빅오표기 : O(x)
• x + logx <= 2x

3. 2^x + 10x^5 + 5x^2

• 빅오표기 : O(2^x)
• 2^x + 10x^5 + 5x^2 <= 22x^2

4. 5x^2 - 6x

• 빅오표기 : O(x^2)
• 5x^2 - 6x <= 5x^2